There are many kinds of two-dimensional spirals, one of the most popular being the Archimedean arithmetic spiral, although not being the most natural. Spirals found in nature are logarithmic, and notoriously the golden spiral based on the Fibonacci sequence. In Illustrator, the standard Spiral Tool only generates logarithmic spirals (there are tricks to create an Archimedean spiral though.)

The Spiral Tool (Illustrator) only builds logarithmic spirals.

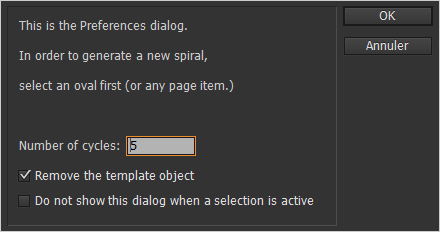
But InDesign provides no way of creating spiraloid stuff at all. So I decided to write a script, DrawSpiral, that instantly draws an Archimedean spiral based on the active selection—which can be an Oval or any frame used as a template. As shown in the demo below, DrawSpiral offers a simple dialog where you can specify the number of desired cycles.

Other dialog options speak for themselves. Disable "Remove the template object" if you need to keep the source object available at the end of the process. By default, the dialog always shows up when you run the script. But if the option "Do not show this dialog when a selection is active" is turned on, then DrawSpiral directly operates on the selection (if any.) Note that your preferences (that is, mainly, the number of cycles) are saved during the current session.

DrawSpiral Preferences Dialog.

DrawSpiral supports from 0.5 to 50 cycles by increment of 1/8th (= 0.125), i.e. 45 degree. This covers a wide variety of spirals, and since these shapes are based on Bézier curves you can play at will with Stroke settings and styles to achieve many interesting effects.

Some spirals at different cycle count.

Technical Note. — Are these spirals perfect from a geometric standpoint? No, they aren't. Archimedean spirals—as well as pure circles!—cannot be exactly reflected into cubic Bézier curves. These are just approximations, and I confess I had great difficulty in determining satisfying control points for the tangent vectors. At each vertex the script calculates the slope and approximates the curve using factors that are involved in emulating circle arcs. Namely, radius × 4/3 × tan(π/16). My method is somehow empirical and I don't pretend it provides the best approximation. (In particular, the eye of the spiral is not as smooth as I would like.)

Have fun anyway!

• See also:
— “Drawing Sine Waves in InDesign”,
— “A Primer on Bézier Curves” by Pomax (M. Kamermans).