Drawing Sine Waves in InDesign [UPDATE]
March 21, 2021 | Snippets | en | fr
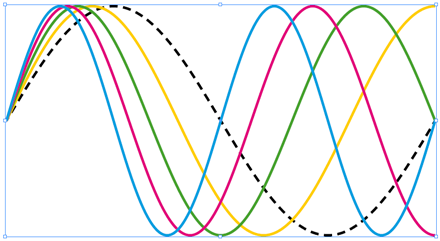
Computing Bézier curves that really look like sine waves is an exciting challenge for script developers. One needs to deal with both optimizing control points, transforming coordinate spaces and splitting curves. Here is a function that solves it all in ExtendScript for InDesign…
Update 21-Mar-2021. — This article and the attached script was originally posted in the “Tips” section due to its technical flavor. However, as the code has evolved and now provides a dialog box that allows the user to easily enter custom settings, the material is now delivered as a standalone script (DrawWave.jsx) that you can just install and use without having to sink into its mathematical arcana…
At its most superficial level, the routine DrawWave.js brings a snippet that takes a PageItem as a canvas and creates a sine wave fitting the target area. This curve is not made of straight-line samples which wouldn't scale smoothly. Instead, we approximate the sine function using a cubic Bézier curve that renders each quarter of the period, 0..π/2, π/2..π, π..3π/2, etc.
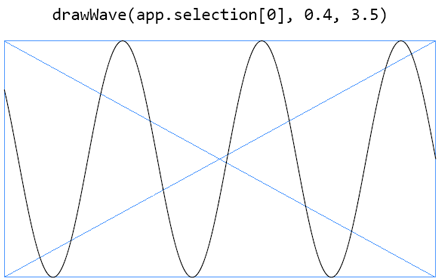
The drawWave() function supports two additional arguments expressing the working interval. Keep the default parameters 0 and 1—that is, drawWave(canvas,0,1)—to generate a full [0,2π] sine wave portion with no phase:

But you can also specify a starting point “in 2π units” (0.25 for π/2, 0.5 for π, etc.) and the final location as well (1 for 2π, 1.5 for 3π, 2 for 4π…). Thus any possible sine curve can be described:
Looking Closer
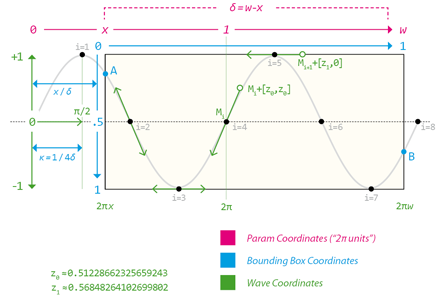
In fact, no Bezier spline can exactly fit each point of an ideal sine wave. One can just provide control points that interpolate slope and curvature in [0,π/2] with minimal error.

Then, given an optimal spline for the first quarter 0..π/2 everything else follows using the symmetry and periodicity properties of the sine function. In this project, however, my goal was to support arbitrary phases within [0,2π[ and arbitrary lengths beyond 2π, including non-integer multiples of π/2. This approach leads to interesting topics:
• Preventing cascading floating-point errors during calculations,
• Translating orthonormal (x,y) coordinates into the specific bounding box system that takes for origin the top-left anchor point and for unit basis the left-to-right and top-to-bottom vectors,
• Locating a point on a cubic Bézier curve, that is, finding the parameter t for which (x(t),y(t)) meets some requirements—in the present case, x(t)==0 for the starting point A and x(t)==1 for the endpoint B,
• Splitting the Bezier curve in A, then in B, without invoking tricky Pathfinder-based operations.
Give a look at the source code to study how these questions have been addressed. Special mention should be made of A Primer on Bézier Curves (by Mike “Pomax” Kamermans), probably the greatest resource ever designed for Bézier fans and programmers. Its “Splitting curves using matrices” section contains all the stuff behind my splitting routine.
Box to Ruler Conversion
As it may happen from time to time on this website ;-) a hidden gem is buried in the script. The function boxToRulerMatrix() takes a PageItem and returns a matrix that maps the bounding box space into the current ruler system whatever the units in use, the zero point, and so on.
This is a powerful helper for those who need to easily generate PathPoint coordinates, or entire paths, from abstract data that only describe the inner geometry of a spline item.
Note that boxToRulerMatrix() invokes a function, parentSpread, which finds the parent Spread of some object. Here is the code of the converter (I use it in many other scripts):
var parentSpread = function F(/*DOM*/o) //---------------------------------- // Return the parent spread of an object, if any { var p = o && o.parent; if( (!p) || (p instanceof Document) ) return null; return ( (p instanceof Spread) || (p instanceof MasterSpread) ) ? p : F(p); }; var boxToRulerMatrix = function(/*PageItem*/o) // ------------------------------------- // Given a page item, return a matrix that maps its // box space (0..1, 0..1) into the current ruler system { const CS_BOARD = +CoordinateSpaces.PASTEBOARD_COORDINATES, CS_INNER = +CoordinateSpaces.INNER_COORDINATES, BB_GEO = +BoundingBoxLimits.GEOMETRIC_PATH_BOUNDS, AP_TOP_LEFT = +AnchorPoint.TOP_LEFT_ANCHOR; var spd = parentSpread(o), ref = spd && spd.pages[0], bo, bs, ro, rs, mx; if( !ref ) return 0; // Box origin --> CS_INNER (trans) // --- bo = o.resolve([[0,0],BB_GEO,CS_INNER], CS_INNER)[0]; // Box (u,v) --> CS_INNER (scaling) // --- bs = o.resolve([[1,1],BB_GEO,CS_INNER], CS_INNER)[0]; bs[0] -= bo[0]; bs[1] -= bo[1]; // Ruler origin --> CS_BOARD (trans) // --- ro = ref.resolve([[0,0],AP_TOP_LEFT], CS_BOARD, true)[0]; // Ruler (u,v) --> CS_BOARD (scaling) // --- rs = ref.resolve([[1,1],AP_TOP_LEFT], CS_BOARD, true)[0]; rs[0] -= ro[0]; rs[1] -= ro[1]; return app.transformationMatrices.add() // Id .scaleMatrix(bs[0],bs[1]) // Box=>Inner scaling .translateMatrix(bo[0],bo[1]) // Box=>Inner transl. .catenateMatrix(o.transformValuesOf(CS_BOARD)[0]) // Inner=>Board .translateMatrix(-ro[0],-ro[1]) // Board=>Ruler transl. .scaleMatrix(1/rs[0], 1/rs[1]); // Board=>Ruler scaling };
• See also:
— The DrawWave basic routine on GitHub,
— “Coordinate Spaces & Transformations in InDesign”,
— Drawing Spirals in InDesign,
— “A Primer on Bézier Curves” by Pomax (M. Kamermans),
— StackOverflow: “How to draw sine waves with SVG+JS?”.

Comments
Heya, small nit: it's far more useful to credit my Primer using "Pomax", not "M. Kamermans" =)
Hi Pomax!
Nickname added. Thanks for your visit ;-)
@+
Marc